The central piece of this blog series will be Jens Rasmussen model of system safety as it pertains to software development. Specifically it will expand on this safety model and clarify, sometimes by analogy with concepts borrowed from other fields, what it means to fail and how we can cope with failure through resilience. In a first step we will overlay the Rasmussen System Safety Model with a more detailed “propensity” map borrowing concepts from Non-linear dynamics, in a second stage we’ll overlay the model with a “causal” map borrowing concepts from the post-structuralist philosopher Gilles Deleuze. I’ll clarify these abstract concept through examples in software development.
The System Safety Model
Rasmussen’s System Safety Model[1] depicts a codified plane of possible states an Operating Point (OP) can move on. These movements are basically decisions/actions made by the actors in the system to increase efficiency or simply to create a product. In software development terms these movements of the Operation Point are for instance commits into the repo and eventually the resulting deploy. All the possible states of the OP are categorised into two distinct planes, the failure plane and the working plane (the plane within the confines of the 3 boundaries). Although this distinction of these planes is purely anthropomorphic it provides us with a certain notion of how decisions in a complex system evolve and how we can decide against hurtful actions. Apart from this binary distinction of fail vs success there are 3 boundaries that separate these planes: the Boundary of Economic Failure (BEF), Boundary of Unacceptable Work Load (BUWL) and finally the Acceptable Performance Boundary or Failure Boundary (FB). It is this last boundary that is of interest in the context of this article since it is the most salient from a software development perspective. (For an excellent explanation of this model watch this presentation).
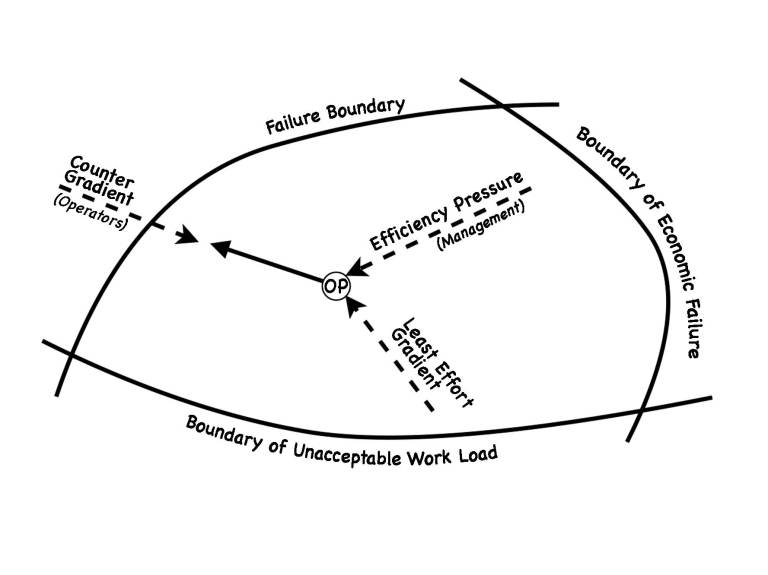
Per Figure 1. the OP gets most often squeezed between the management gradient and the least effort gradient. Management (aka the blunt edge) has the tendency to pressure the operators (aka the sharp edge) into a more economic efficient regime (for instance make the workers do their job with limited resources). On the other hand there is the least effort gradient. If you fall below this line your workers drop from exhaustion (basically everybody sleeps below this line). If there are no counter forces to oppose these tendencies the OP is constantly moved toward the Acceptable Performance Boundary. Counter forces, most often actuated by the sharp edge, like actionable safety rules, regulations, checks and whatnot keep the OP into the working plane.
This simplified model of Rasmussen presupposes a neutral plane in which the decision device “transports” the OP on a Brownian-like path. In reality the plane consists of a surface “pre-organized” by attractors and bifurcations. In this article we will investigate how jagged this surface is and how known problems in software development map onto this rugged plane.
Attractors & Bifurcations
Pointcaré discovered and classified certain special topological features of two-dimensional manifolds (called singularities) which have a large influence in the behaviour of the trajectories, and since the latter represent actual series of states of a physical system, a large influence in the behaviour of the physical system itself.[1]
Developing a software products entails making many decisions in a very dynamical environment. These decisions often affect future possibilities, make past decisions superfluous or in need of refining while the whole space of decisions (aka Git-commits) is in constant movement through requirement changes. While all this is going on, a software development team runs through this dynamic system in cyclic way (sprints), searching through this space of decisions states, making the system as effective/flexible as possible while hopefully not encountering a failed state. Since this description of how software development works is an instance of a complex adaptive system and it can be equated with what is called a State space search (in artificial intelligence). This process can be historically traced back to a mathematical representation called the Pointcaré map. Henri Pointcaré, being the pioneer of this mathematical approach to dynamical systems did not use differential equations to model real physical systems but used a model called State Space to explore the recurrent traits of any model with two degrees of freedom, like a swinging pendulum for instance.

This example of State Space representation is in fact a map of every state the system can possibly be in and represents each state in the system as a vector (propensity to evolve into the next state). In 3D the graph in Figure 1. would look like a basin (aka attractor or singularity) with the bottom of the basin representing the state of equilibrium. As for our description of software development you’d have to imagine a rugged landscape with lots of tops and basins that are constantly changing when the “Operating Point” moves from one state to the next. Another interesting concept that can be derived from the dynamics of the State Space is a bifurcation. This phenomena occurs when the “Operating Point” is moved to some area of the State Space which has the effect of a qualitative or topological change in its behaviour. Another example of a bifurcation (or in stochastic terms a State Transition) is the series of state transitions water undergoes while being heated. From ice to liquid and steam for instance (or within the liquid form: from laminar flow to convection to turbulence). These are examples of a cascade of symmetry breaking phase transitions and represent real qualitative changes within the system.
So when we overlay the map of System Safety Model with the State Space we get a more codified version of Rasmussen’s model. We can begin to identify certain areas in the model that have dangerous basins (read Technical Debt or just plain bad decisions) close to the different boundaries in Rasmussen’s model that are hard to get out of or where the whole system (read team) changes for the better into a qualitative (read more productive/resilient or the sometimes 4-fold increase in productivity in a Scrum-team) area of the State Space.
Of course these statements presume that your software development team exhibits adaptive behaviour, is diverse and shows connectedness or efficient communication for the system as a whole to be in a complex state. Wolfram[4] states that any given system can be in one of 4 states: equilibrium, cyclic, chaotic or complex. Hopefully your team does exhibit complex or some cyclical behaviour and not the other 2. If your team is constantly at equilibrium you must ask yourself if any code at all is being written and if they are chaotic you’ll be driven nuts by now.
Besides the great simplification achieved by modelling complex dynamical processes as trajectories in a space of possible states, there is the added advantage that mathematicians can bring new resources to bear to the study and solution of the physical problems involved.[2]
Ghostly Operating Points Through Technical Debt
Although not scientifically proven, Technical Debt as described by Ward Cunningham is a great way to investigate the saneness of a software development project. As for the model we are exploring, Technical Debt undoubtedly introduces drag for the OP.
So when Technical Debt creeps into your system it doesn’t necessarily cross the APB per se, it simply makes the basin of the State Space deeper. Although it normally requires an enormous economic effort to drag the Operating Point out of this virtual failure, it doesn’t mean the system as a whole failed. It just makes it harder for the sharp edge to move back the OP within the acceptable boundaries. So Technical Debt is an attractor/singularity into a virtual failure state (it makes it easier for future decisions to fail and is hard to bifurcate out of) if you like. Counter forces like conformity, testing and modularisation make those basins less deep and are gentler to the OP. These measures dampen the effects that negative/deepening decisions have on the OP thus making your organisation more resilient. More on resilience later in part III of this series.
Conclusion
In contrast to the simplified plane version of the Rasmussen model, where the boundaries and the plane it devides are smooth we’ve come to show that identifying the “jaggedness” of the search-plane can help to identify points-of-no-return and stabilising attractor points on the map. Furthermore it helps to think in terms of drag-introducing (or basin deepening) actions or bifurcating decisions for the benefit of the OP. In the next post I’ll zoom in on failure and analyse what it really means on a causal level and how to cope with it in a meaningful way.
- 1. Jens Rasmussen – Risk management in a dynamic society: a modelling problem (1997 – http://www.sciencedirect.com/science/article/pii/S0925753597000520)
- 2. & 3. Manuel Delanda – Intensive Science & Virtual Philosophy (2002 – Continuum Books)
- 4. Stephen Wolfram – A New Kind Of Science (2002 – Wolfram Media)
